We demonstrate some interval methods for zeros of functions of one or several variables.
Let us start with a simple example. Solve x^2=2.
>function f(x) &= x^2-2
2
x - 2
We need the derivative for the Newton algorithm.
>function df(x) &= diff(f(x),x)
2 x
We start with the interval [1,2].
>X=~1,2~
~1,2~
The Interval Newton Method is the following iteration.
Xn = X && ( m - f(m)/f(X))
It stops, if X=Xn. If X contains a zero, Xn does too. The inclusion is guaranteed, if (m-f(m)/X is a subset of X. The computation must be evaluated in interval terms, of course.
>repeat m=middle(X); Xn=X&&(~m,m~-f(~m,m~)/df(X)), until Xn==X; X=Xn; end;
~1.37,1.44~ ~1.414,1.4145~ ~1.414213559,1.414213566~ ~1.4142135623730947,1.4142135623730954~ ~1.4142135623730947,1.4142135623730954~
Since the result is a proper subset of the interior of the start interval, we have a guaranteed inclusion.
Euler implements this in the function inewton2, which takes two functions of vectors f and df, or two expressions.
>inewton(f,df,2)
~1.4142135623730947,1.4142135623730954~
The function mxminewton computes the derivative with Maxima.
>mxminewton(&f(x),~1,2~)
~1.4142135623730947,1.4142135623730954~
There is a simple function ibisect, which runs the bisection algorithm carefully to guarantee an inclusion of the solution.
>ibisect(f,1,2)
~1.414213562373094,1.414213562373096~
Let us try another example.
>function f(x) &= tan(x)-x
tan(x) - x
We can use the bisection algorithm starting with a course interval.
>res1=bisect(&f(x),0,1,y=1e-20)
3.10506038659e-007
How accurate is this result?
Indeed a plot shows that the cancellation in tan(x)-x destroys the accuracy of the function, and thus the accuracy of the zero.
>plot2d(&f(x)-1e-20,0.99*res1,1.01*res1,adaptive=0):
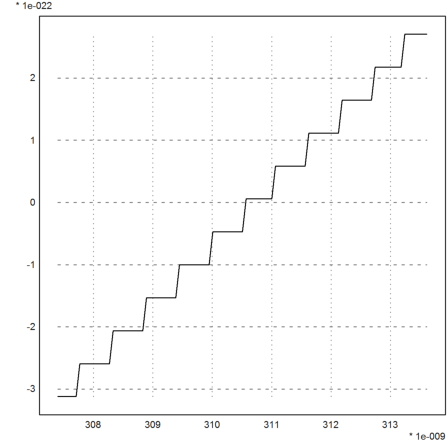
The function ibisect stops early.
>ibisect(&f(x),0,1,y=1e-20)
~3.091e-007,3.111e-007~
The Interval Newton Algorithm is not much better.
>mxminewton(&f(x),~1e-7,1e-6~,y=1e-20)
~3.1015e-007,3.1116e-007~
To get a better result, we need to approximate the function with its Taylor series, which can be evaluated very well.
>function f(x) &= taylor(tan(x),x,0,10)-x
9 7 5 3
62 x 17 x 2 x x
----- + ----- + ---- + --
2835 315 15 3
>mxminewton(&f(x),~1e-7,1e-6~,y=1e-20)
~3.1072325059538179e-007,3.10723250595382e-007~
Strictly, we have not solved tan(x)=x here. We need to add an error term to be precise. The error of the Taylor series is
f^(11)(xi)/11! x^11
with some xi between 0 and x.
>function dtan11(x) &= diff(tan(x),x,11);
We add the error term to f.
>function fi(x) := f(x) + dtan11(0||~x~)/11!*x^11
Now we get an exact and guaranteed solution.
>ibisect("fi",1e-7,1e-6,y=1e-20)
~3.1072325059538174e-007,3.1072325059538211e-007~